To develop an effective options trading strategy, you need more than just an understanding of price movements; you must also grasp how various risk factors impact your options contracts. The Greeks, critical metrics in options trading, play a crucial role in this. They are numerical indicators that measure an option’s sensitivity to factors such as the underlying asset’s price, time, volatility, and interest rates. Metrics like Delta, Gamma, Theta, Vega, and Rho provide deep insights, enabling you to manage risks effectively and optimize your trading strategies.

Understanding Options Contracts

Options contracts are essential for managing investment risks and speculating asset price movements. Traders use options for two primary purposes:

Hedging: Options can protect a portfolio by offsetting potential losses from unfavorable market movements.

Speculation: Traders use options to bet on whether an asset’s price rises or falls.

Here’s a breakdown of the two types of options:

Call Option: This option grants the holder the right, but not the obligation, to buy the underlying asset at a specific price.

Put Option: Grant the holder the right, but not the obligation, to sell the underlying asset at a predetermined price.

Options can be exercised, meaning the option holder can convert them into shares of the underlying asset at the agreed-upon strike price. Each option has an expiration date and a premium, which is the cost or value associated with the option. The price of an option fluctuates based on an option pricing model, such as the Black-Scholes model, which factors in various market conditions.

The Role of Volatility in Option Pricing

Volatility refers to how much an option’s market value fluctuates before expiration. Various factors contribute to this fluctuation, including a company’s financial health, economic conditions, geopolitical risks, and overall market movements.

Implied volatility reflects the market’s expectations regarding future price changes of an asset. Investors use implied volatility to predict the future movement of the underlying security and the corresponding price of the option. If implied volatility increases, an option’s premium is likely to rise as well.

Assessing Option Profitability

Options can be classified as profitable or unprofitable depending on the relationship between the strike price and the underlying asset price. This difference is referred to as intrinsic value.

At-the-money (ATM): The strike price equals the cost of the underlying asset.

In-the-money (ITM): The option has intrinsic value, as its strike price is more favorable than the asset’s current price.

Out-of-the-money (OTM): No profit is made since the strike price is less favorable than the underlying asset’s price.

Factors Influencing Option Prices

Options prices, including call and put options, are influenced by several key factors. One of the most significant is implied volatility, where an increase or decrease in volatility can lead to higher or lower option prices. Specifically, when implied volatility rises, option prices tend to increase because market uncertainty boosts the value of options. Conversely, when volatility decreases, option prices may drop.

In addition to volatility, the time to expiration plays a crucial role. Options generally have higher values when there is more time left until expiration, as there is more significant potential for the underlying asset’s price to move. As expiration approaches, option prices may decrease due to the limited time for price changes.

Finally, the underlying asset price has a significant impact on option prices. When the underlying asset’s price rises, call options become more valuable, while put options lose value. Conversely, when the underlying asset’s price falls, put options gain value.

What are Options Greeks?

In options trading, “the Greeks” refer to measures used to assess the sensitivity of options and other derivatives to critical factors such as the underlying asset’s price, time decay, volatility, and interest rates. These factors are crucial in understanding and managing the risks associated with options positions. Named after letters from the Greek alphabet—Delta, Gamma, Theta, Vega, and Rho—each Greek represents a specific aspect of risk in the market.

For example, Delta measures an option’s price changes in response to price movements in the underlying asset. At the same time, Theta quantifies the time decay of an option’s value as it approaches expiration. Similarly, Gamma and Vega assess how price movements and volatility impact an option’s value, and Rho looks at how interest rate changes can affect the price.

Traders rely on these measures to monitor and adjust their positions. Since the value of each Greek fluctuates over time, sophisticated traders calculate them regularly to keep track of changes and manage risk effectively. Understanding the Greeks is essential for making informed decisions and optimizing strategies in options trading.

Delta

Delta in options trading is a crucial indicator that helps investors assess how an option’s value changes when the price of the underlying asset changes. Specifically, Delta shows the degree of fluctuation in the option’s price when the price of the underlying asset changes by $1. The value of Delta ranges from -1 to 1, with call options having Delta between 0 and 1 and put options having Delta between 0 and -1.

For example, buying a call option with a delta of 0.50 means that if the underlying asset’s price increases by $1, the option’s value will increase by $0.50. On the other hand, if you buy a put option with a delta of -0.50, this means that when the underlying asset’s price decreases by $1, the value of the put option will increase by $0.50.

Delta not only helps determine how sensitive an option is to changes in the underlying asset’s price but also changes over time and based on the option’s value. Options at or in the money typically have higher Delta, meaning they will move more significantly when the underlying asset’s price changes. Conversely, out-of-the-money options have lower Delta, meaning they are less sensitive to price fluctuations in the underlying asset.

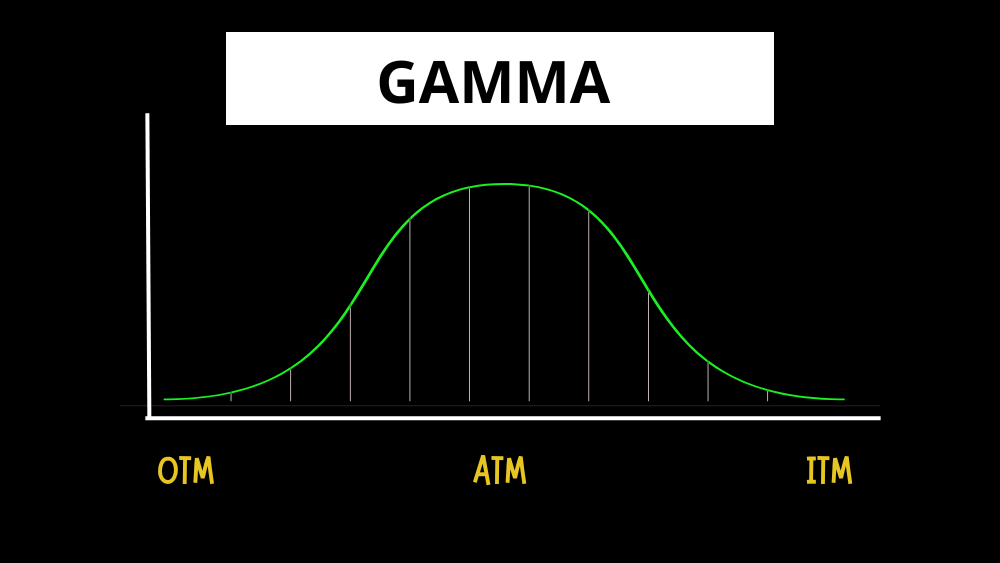
Gamma

Gamma is an essential metric in options trading that measures the rate of change in Delta as the price of the underlying asset moves. While Delta shows how much an option’s price will change with a $1 move in the underlying asset, gamma tells you how much Delta will change as the asset’s price fluctuates. This makes gamma essential for understanding how stable or volatile the Delta will be, allowing traders to better assess risk and potential price movements.

Gamma is typically highest for at-the-money options because these options are most sensitive to price changes. As the option becomes further in- or out-of-the-money, gamma decreases. This is because the price changes impact the option’s price less when it is deep in or out of the money.

For example, consider two options with the same delta value: one with a high gamma and one with a low gamma. The option with the higher gamma will experience more significant shifts in delta as the price of the underlying asset moves. This means the choice is riskier, as it will likely experience large price swings. On the other hand, options with low gamma are more stable, making them more predictable for traders who prefer less volatility.

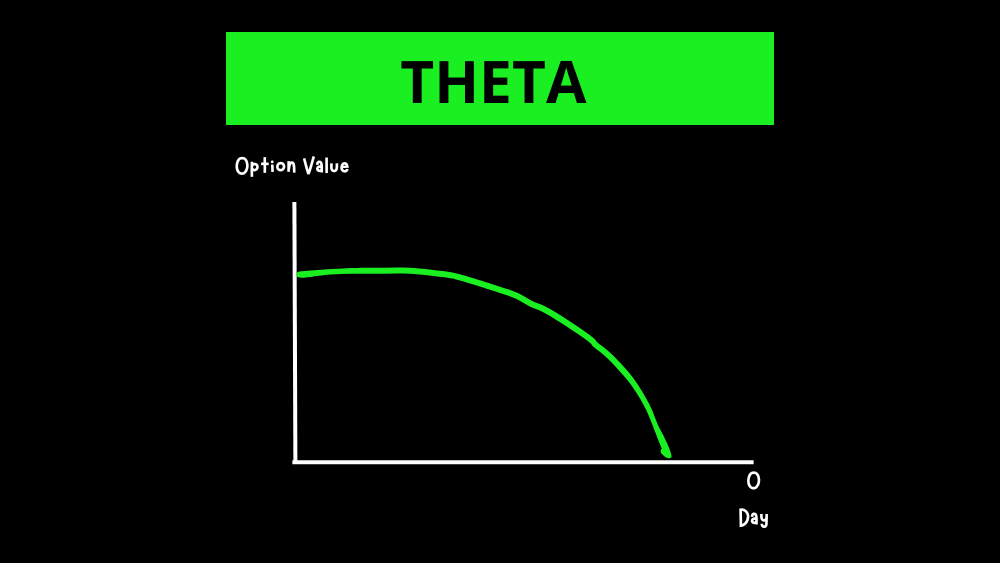
Theta

Theta measures the time decay of an option’s value, meaning that the value of the option decreases as time passes, even if the underlying asset’s price does not change.

For example, if a call option has a theta of -0.05, this means that for each day that passes, the option’s value will decrease by $0.05, assuming the underlying asset’s price does not change.

 

Time decay is not uniform. As the expiration date approaches, the rate of time decay accelerates, making options lose value faster as they get closer to expiration.

Vega

Vega measures the change in the price of an option when implied volatility changes by 1%. Implied volatility reflects the market’s expectation of future volatility of the underlying asset. When implied volatility increases, options become more expensive because there is a higher probability of reaching the strike price. Conversely, when implied volatility decreases, options become cheaper.

Vega helps traders understand how changes in implied volatility impact the price of options. For example, if you hold a call option on XYZ stock and the implied volatility of that stock increases by 1%, the value of your option may rise, allowing you to profit if the stock price increases significantly. However, if implied volatility decreases, the value of your option will decrease, reducing the value of your position.

Vega changes over time as well. Options with longer expiration periods will have higher Vega because changes in implied volatility have a more significant effect on the value of the option over a longer period. However, as the expiration date approaches, Vega decreases because changes in implied volatility have less of an impact on options in a shorter time frame.

Rho

Rho measures the sensitivity of an option’s value to changes in the risk-free interest rate. This rate is typically expressed as the change in the option’s value when interest rates change by 1%. Rho has a greater impact on long-term options compared to short-term options, as a longer time to expiration means that interest rates will have a more significant effect on the cost of maintaining the position.

Rho is positive for call options, meaning that when interest rates rise, the price of the call option tends to increase. Conversely, Rho is negative for put options, meaning that when interest rates rise, the price of the put option tends to decrease.

FAQs